Principi di Kirchhoff - Un Esempio
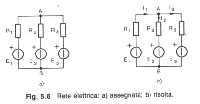 Risolvere la rete elettrica della fig. 5.6 mediante i principi di Kirchhoff.
Risolvere la rete elettrica della fig. 5.6 mediante i principi di Kirchhoff.
Dati: E1=10 V, E2= 5 V, E3 = 4 V, R1=10 Ohm, R2 = 10 Ohm, R3 = 20 Ohm.
Determinare le tensioni e le correnti.
Soluzione
Essendo i lati l=3, nodi n=2, maglie m=3, le equazioni indipendenti risultano:
- per i nodi: n-1=1
- per le maglie: l.n+1=2
Ipotizzando il senso delle correnti convergenti al nodo A si ha:
equazione al nodo A: I1+I2+I3=0
equazione alla maglia 1,2: E1-E2=R1 I1-R2 I2
equazione alla maglia 1,3: E1-E3=R1 I1- R3 I3
Sostituiamo i valori dati e semplifichiamo:
Sistema
{
I1+I2+I3 = 0
10-5 = 10 I1 - 10 I2
10-4 = 10 I1 - 20 I3
}
Sistema
{
I1+I2+I3 = 0
5 = 10 I1 - 10 I2
6 = 10 I1 - 20 I3
}
Sistema
{
I1+I2+I3 = 0
1 = 2 I1 - 2 I2
3 = 5 I1 - 10 I3
}
Dalla seconda equazione si ricava: I2 = (2 I1 - 1) / 2
Dalla terza equazione si ricava: I3= (5 I1 -3) / 10
Sostituendo nella prima:
I1 + [(2 I1 - 1) / 2 ] + [(5 I1 -3) / 10] = 0
Operando e semplificando: 10 I1 + 10 I1 - 5 + 5 I1 -3 = 0
25 I1 = 8
I1 = 8/25 = 0.32 A (Verso A)
I2 = ( 2 * 0,32 -1 ) / 2 = -0,18 A (Verso B)
I3 = ( 5 * 0,32 -3) / 10 = -0,14 A (Verso B)
Dalla fig. 5.6b si desume che:
E1 Ŕ un generatore
E2, E3 sono utilizzatori attivi.
La tensione fra i nodi A e B puo' essere determinata indifferentemente con rifermineto ad uno qualsiasi dei tre lati. Si ottiene infatti:
V = E1 - R1 I1 = 10 - 10 * 0,32 = 6,8 Volt
V = E2 + R2 I2 = 5 + 10 * 0,18 = 6,8 Volt
V = E4 + R3 I3 = 4 + 20 * 0,14 =6,8 Volt
Giovanni Ceglia
giovanniceglia@xungame.com


